Motorcycle Springs Advanced | ProMechA Motorcycle Suspension

Springs Advanced III

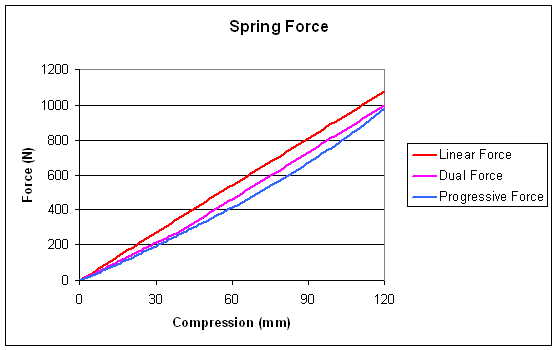
The graph above shows how much force is required to compress each of three different types of spring a certain amount. You just look up the amount of compression along the bottom edge, move vertically up until you hit the appropriate colour line (as per the list at the right), then move horizontally across to read off the force.

The feature that is immediately obvious is that the graphs all go up as they go right: more compression means more force. Makes sense, right?

The three spring types are linear (ordinary); dual rate (often called "progressive") and progressive (really!). The ordinary one has a rate of 9N/mm, so to get compressed 120mm it needs 120 x 9N of force, or 1080N. Note that the graph is a straight line, which is why it’s called linear.

Dual rate springs are made by putting a short spring with closely wound coils on top of a longer spring. Initially, when you apply a force it acts on both springs and they both compress. So the total compression is more, for the same force, than either spring alone. That means it has a softer rate. If you don't like formulae, just ignore the next sentence. If you don't mind, the combined rate is K=K1 * K2 / (K1 + K2), where K1 and K2 are the rates of the individual springs.

However, after some compression, the closely wound spring jams solid as all the coils come together (it "coil binds"). So now you only have a single spring, which we’ve already said is stiffer than the combined springs. In the example above, the combined springs have a rate of 7N/mm, while the second spring has a rate of 9N/mm. The first spring coil binds at 40mm: you can see a kink in the graph at that point. Note that the two springs can be made from the same piece of wire: all that matters is that their coils have different spacing. By the way, the above numbers mean that the initial part of the spring must have a rate of 31.5N/mm: it’s wrong to suppose that the first part is a soft spring!

While many people call dual rate springs progressive, true progressive springs have gradually increasing coil spacing, so that the coils bind up one by one. So if you look at the plot for the progressive spring above there is no sudden change in slope, it just gradually curves upward.

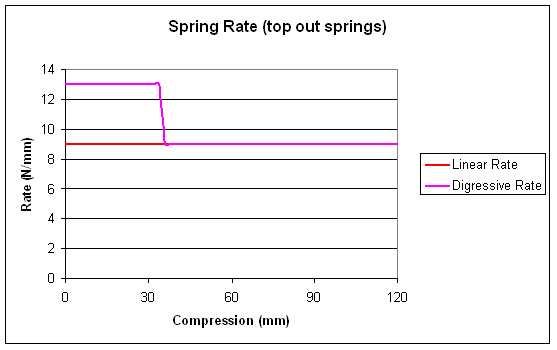
Graphing the rate

So how do I read spring rate from the graph?

Remember that rate is the amount of additional force to compress the spring an extra 1mm. Or in other words, how far the graph moves up for 1mm to the right… or its slope. The linear spring has the same slope all the way, the dual rate changes slope after 40mm, while the slope of the progressive spring increases gradually all the way.

We could just graph the slopes directly, which makes things clearer:

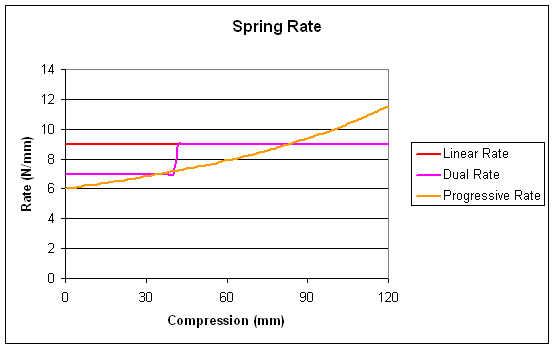
The only danger of looking at this is that the sudden step at 40mm looks a bit scary, which it actually isn't.

Would you like preload with that?

So what happens if we add preload? All that means is we have already compressed the spring a bit before we start measuring. On the force graph it looks like we’ve moved things up, but in fact we’ve moved them to the left. Check the position of the kink in the dual rate spring to see this. The graphs below have 15mm preload.

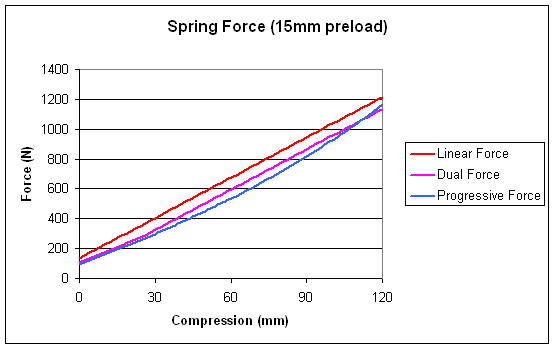
It's a little clearer on the rate graph: the linear spring rate doesn’t change at all, while the others just shuffle across to the left a little.

Digression

No, I'm not going off on a tangent. Springs that get softer as they go down are called digressive. I guess it sounds better than regressive and the political metaphor doesn’t work: all springs are technically conservative, which means they store energy and return the full amount.

We actually discussed digressive springs back in part 2 (Sag and Preload), where I called them top-out springs. We arrange one spring pushing up and one pushing down, opposing each other. That means their rates add, K=K1 + K2. Now if you press down far enough, the upper spring will reach its free length and just stop doing anything. At that stage you only have K2, but this time it’s smaller than the combined rate. What I’ll show below are the force and rate graphs for a 9N/mm main spring, with a 4N/mm top-out spring which extends 35mm before giving up.

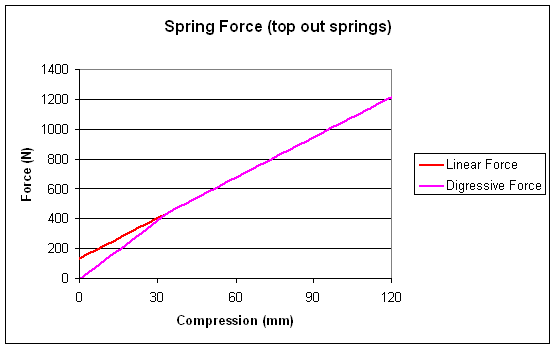
Notice that initially less force is required, although the slope is steeper.

One perverse question you might have at this stage: what if I combine a dual-rate main spring with a top-out spring? The rate would either go down then up again, or up then down, depending on the relative lengths of the various spring components.

Honda actually used this set-up on their CBR600RR!

Is it a good idea then?

I’ve already explained why top-out springs make sense, although now I can just point to the force graph above: less force is required to move the suspension when it is lightly weighted, such as when accelerating out of a corner.

Progressive springing is much less popular for road-racing, with linear main springs used almost universally. There is a good reason for this: going around corners compresses your suspension, by quite a lot with modern race tyres. With progressive or dual rate springs, that means the suspension is going to be stiffer than when upright. However mid corner is also where you most need good grip and would really prefer your tyres not to be bouncing off the ground.

This has led to a more extreme form of digressive suspension, where the rate changes below the rider-sag point. In principle this can compensate for high lean angle and provide better mid-turn grip. Typically it’s achieved via a linkage system at the rear: the 2004/5 ZX10R has a weakly digressive rear suspension. Also, Honda introduced a significantly digressive rear suspension on their 2001 RS250 race bike, replacing the strongly progressive system on the 2000 and earlier models. Both suffer from problems driving out of corners. After-market race-kit manufacturer quickly provided alternative linkages for the RS250, while the ZX10R can be made linear with some longer dog-bones and a spacer under the top shock mount. There’ll be more about linkages in a later article.

Dual or progressive rate springs are really a compromise that allows low-speed comfort without excess bottoming, which is why Honda fit them to road bikes. Racing is not about compromise, so they don’t get used for that.

Dirt bikes may be another matter, since they need to cope with jumps and big, big bumps. However there is still a problem: it's desirable that your suspension is configured with damping to match your spring rates. Rebound damping in particular needs to be stronger to prevent a stronger spring from recoiling. However if the spring rate changes, it's tricky to make the damping change to suit. KTM have some tricks for doing it on their PDS dirt bikes, with limited success.

There are other ways of achieving variable rate rear suspension, via linkage systems as mentioned above. I'll discuss them in a future article, along with the role of air and oil height in forks.

Summary

If we graph force versus position we can see the effect of different spring types. The slope of the graph is the spring rate.
We can arrange springs so that the spring rate increases (progressive), decreases (digressive) or remains constant (linear) through the suspension stroke.
Progressive or dual-rate suspension is a compromise for comfort, it's not ideal for race-track use.

You've probably heard of progressive springs. They sound like a good idea, I mean who wouldn't want to be progressive? How many conservative springs would sell to motorcyclists?

Before we talk about whether they’re good or not, we need to understand what they are. To do that, life will be much easier with graphs. Some of us who work with numbers all our lives tend to forget that some people didn’t master basic X-Y graphs at the same time as walking, but I'll try to lead you through this a bit.